Mathematics

Project  

Many real-world systems can be described as networks of coupled oscillators, such as neurons in the brain, the dynamics of power grids, and the flashing of fireflies. Common to all these systems is spontaneous synchronisation, such that an ordered synchronised state emerges from a disordered state. What is different among coupled oscillator systems is how the synchronised state is reached.

The role

In this project you will explore synchronisation phenomena through a combination of mathematical analysis and numerical simulation.

Project  

We are all very familiar with contagions. As well as disease spread, contagions describe many other spreading processes, such as the spread of information/disinformation. Simple contagion models, such as the SIR-model, assume a well-mixed population.

The role

In this project you will break that assumption, and study contagion models on complex networks, where network nodes are individuals, and network edges are interactions. This project will combine mathematical analysis and numerical simulation to study the role of network structure on contagion dynamics.

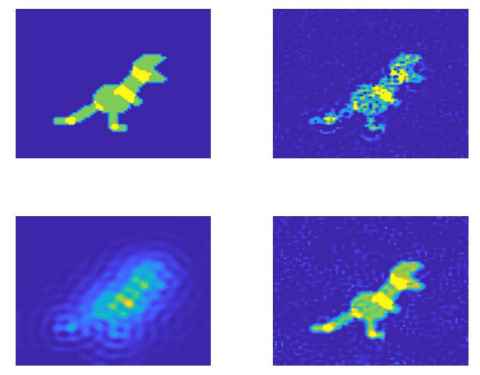
Project  

The aim is to locate the source of some sound, here we imagine to locate an island from the noise of its inhabitants. Typically, microphones are located randomly in the ocean surrounding the island to measure the roars.
This is called an inverse source problem and it requires to invert a non-invertible (not even square) matrix to reconstruct a large dimensional image from only few measurements data (microphones).

Pre-requisites

MATHS 260, MATHS 270, possibly MATHS 361, 362 or 363

Project  

Interactions between species, such as predator-prey or competition, are often modelled using simple Lotka-Volterra type differential equations. Such models are an idealisation, and ecologists are interested in the effect of higher-order interactions.

The role

This project will use dynamical systems methods to investigate and classify the qualitative effects on the dynamics of higher-order interactions in two- and three-species models.

Prerequisites

Maths 260, and at least some programming experience.

Project  

Networks of coupled oscillators arise in a wide range of physical applications, and the dynamics of the system is constrained at least in part by the connectivity and topology of the network.

The role

This project will investigate how the topology of the physical network affects the existence of objects called heteroclinic networks in the resulting phase space.

Prerequisites

Maths 260, and at least some programming experience.

Project  

Everyone has a story about learning mathematics. Many of these are happy stories. But some are not. For some people, mathematics is so tinged with distress and confusion that they opt out of the subject as soon as they can, avoiding it into adulthood, often at personal cost.

The role

This project explores how stories might be used to invite mathematics-averse adults to reconnect with the subject. It will involve searching and reviewing research literature, and analysing data.

Ideal student

Experience in MATHS 302 is useful.

Project  

Translation surfaces are formed by glueing polygons along their edges, ensuring that the glued edges are translated copies of each other. Alternatively, they can be defined using mathematical concepts like holomorphic differentials on Riemann surfaces, or flat metrics on surfaces with prescribed singularities.

These equivalent perspectives give rise to a rich theory that combines several branches of mathematics, including topology and complex analysis.

The role

The goal of this project is to learn about translation surfaces and explore some of their properties.

Project  

Given n, what is the smallest degree of a polynomial identity valid for all pairs of n×n matrices? This is a problem in noncommutative ring theory.

The role

The aim is to investigate the structure of identities, and use it to simplify the search for minimal ones. The desired outcome is answering the starting question for small n.

Prerequisites

Maths320, enthusiasm about advanced linear algebra, and willingness implement algorithms with a symbolic computation software (like Mathematica, Maple or Magma).

Project  

An undirected graph is geodetic if every pair of vertices has a unique path of shortest length between them. There is a conjecture that the only finite geodetic Cayley graphs are odd cycles and complete graphs.

The role

The goal of this project is to explore this conjecture, either theoretically or through computations.

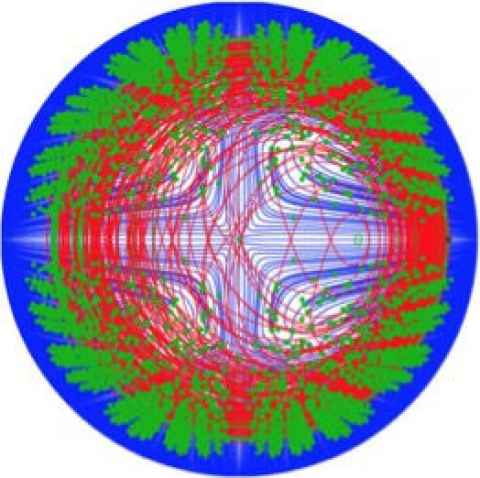
Project  

Wild chaos is a new form of unpredictable behaviour that can occur in higher-dimensional dynamical systems. Only very few examples are known, but a previous summer project student discovered a measure of wild chaos that can identify such behaviour in experiments.

The role

Your task will be to test the approach on data that is thought to come from a wild chaotic attractor in a three-dimensional discrete dynamical system, defined by a map. If it works, what happens as parameters change and wild chaos is lost?

Prerequisites

Maths 260 and good Matlab or Python coding skills.

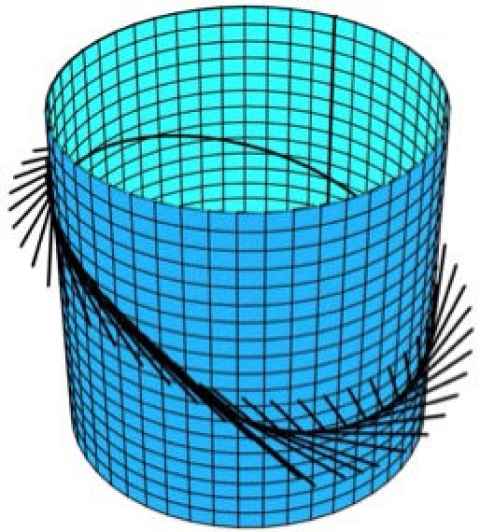
Project  

Chebfun is an extension to Matlab that allows for arithmetic operations on functions, performed to machine precision, using Chebyshev polynomials. Recent updates include periodic function approximations.

The role

Your task will be to develop a new application of Chebfun for the computation of an invariant closed curve, or torus, in a two-dimensional discrete dynamical system, defined by a map. In two dimensions, the torus will be either attracting or repelling.

Are you up for the challenge of doing it for a three-dimensional system when the torus can be of saddle type?

Prerequisites

Maths 162, Maths 250, and good Matlab coding skills

Project  

Pursuit–evasion games are a family of two player games in mathematics and computer science in which one player attempts to track down or capture another player in an environment. There are countless variants of these games, depending on the environment, the precise rules of how players move, the information available to each player, and various other parameters.

The role

In this project, you will study pursuit evasion games that take place on a graph, and in particular the effect of random moves on the game.

Ideal student

The project is suitable for students who have enjoyed an introduction to combinatorics (e.g. COMPSCI225), some background in probability theory and programming skills will be an asset.

Project  

Tipping points in dynamical systems are rapid transitions between two distinct states. In a physical sense, one might think of ecosystem collapse, or rapid changes in climate systems. In a mathematical sense, tipping points can be driven by noise, or bifurcations. Depending on the type of tipping point, there are different warning signals which will occur prior to the tipping point, which may be useful for managing these systems. (Most interest to date has been in applications to climate or ecology.)

The role
This project will focus either on tipping points in spatial systems, or application of tipping points to physiological systems (asthma in particular), depending on the interests of the student.

Ideal students

Interested students should have at least some background in differential equations and bifurcations (maths 260 or similar) and numerical methods (maths 162, 270 or similar).

Project  

Suppose that, from some observable dynamical system, we have only a set of observations of this system at discrete times. The problem of equation discovery is: can we reconstruct, from these observations alone, the dynamical system which governs the underlying behaviour of this system?

The role

Importantly, we want not just to predict the future time course beyond the observations (i.e. in a black-box fashion) but to gain understanding of the underlying system; in the case of a system of differential equations, can we reconstruct the underlying equations themselves given only the observations?