Liver Modelling Group

We use multiscale modelling techniques to simulate hepatic surgery, circulation, drug uptake and clearance under healthy and pathological conditions.

Surgical planning for liver surgery

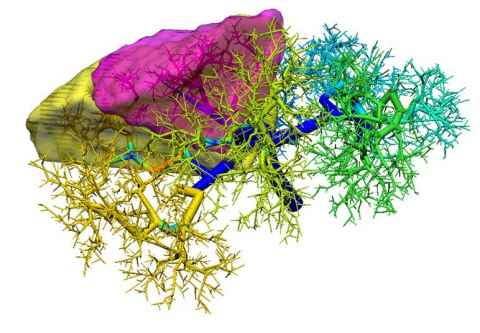
Progresses in fast simulations of the hepatic flow in subject-specific vascular trees have provided new opportunities for pre-surgical planning. We have developed an in silico computational pipeline that integrates several recently developed multi-dimensional blood flow modelling algorithms. Firstly, a semi-automatic segmentation pipeline is used to digitise hepatic vessels. Then, a constructive constraint optimisation (CCO) algorithm is used to extend the digitised vascular tree, and also to compute the blood pressure and flow velocity in the tree (Fig. 1). Couinaud segments are simulated from the diffusion zones of the portal venous tree. The constructed surgical planning model is then deployed cross-platform (desktop or mobile phones) for use in various scenarios. This in silico pipeline has been used to simulate hepatic flow variations pre- and post-liver surgery and transplantations.

Fig. 1: CCO algorithm is used to extend the portal veins and to simulate the Couinaud segments. There are ~8,000 vessel segments in this portal tree.

Modelling the drug transport, uptake and clearance in liver lobules

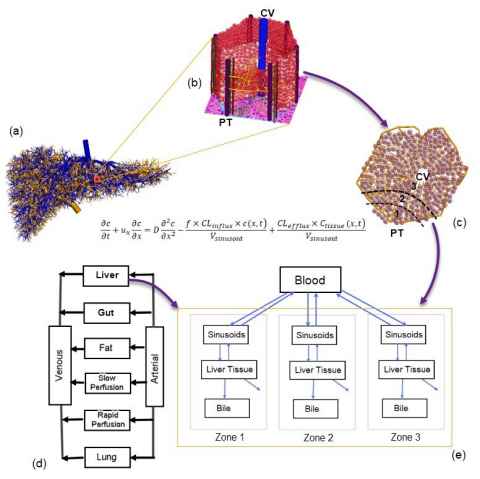
We are developing virtual lobule models with the aim to bridge biomechanical models of blood flow and pharmacological models in the liver. We are particularly interested in modelling the spatial heterogeneity of metabolism enzymes and transporters. Hepatocytes in a lobule are conventionally grouped into three metabolic zones (Fig. 2). Such a zonal differentiation is crucial in spatially heterogeneous diseases. For example, an overdose of the painkiller acetaminophen may lead to hepatotoxicity and necrosis of hepatocytes, which mostly occur at Zone 3.
We have developed a multiscale virtual lobule model whereby the sinusoidal flow is simulated with a partial differential equation accounting for the diffusion and advection of chemical species. Ordinary differential equations are used to quantify the metabolism and clearance in hepatocytes or liver tissue. In this way cellular and intra-cellular dynamics are coupled. This approach can be applied in a number of hepatology studies, e.g. to describe the glucose homeostasis where the metabolism kinetics of glucose, lactate and glycogen is coupled with the finite element model of sinusoids. The zonal hepatotoxicity due to the overdose of acetaminophen is simulated in a similar manner. Since each hepatocyte has its own set of enzymatic parameters, hepatocytes can be modelled as an agent-based system.

Fig. 2: A numerical scheme for multiscale biomechanical and pharmacological modelling for the liver: (a) Vasculatures generated from the CCO algorithm range from root vessels to portal triads at the peripherals of liver lobules; (b) a 3D representation of the liver lobule; (c) a 2D cross-section of the liver lobule, highlighting the three metabolic zones; (d) a PBPK model where the liver is modelled as a “well-stirred” organ; (e) a compartmental model for drug clearance in the liver organ incorporating metabolic zonation. In the listed equation, sinusoid-tissue influx/efflux terms are added to the transport equation of drugs for ODE-PDE coupling.

Modelling the hepatic B virus (HBV) kinetics

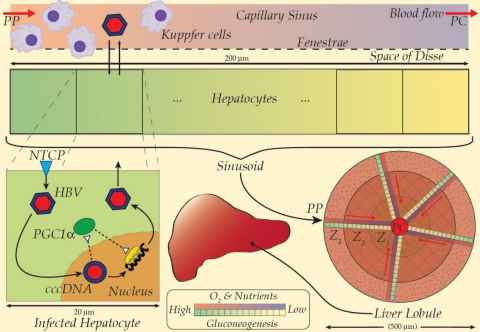
For nearly 250 million people worldwide suffering from chronic hepatitis B virus (HBV) infection, there are few effective options for treatment. Elimination of HBV from liver tissue remains an elusive goal; chronic HBV is exceptionally difficult to treat. It results mainly from maternal-neonatal vertical infection but also in roughly 5% of horizontal infections, and is characterised by the entrenchment of viral covalently closed circular DNA (cccDNA) in host nuclei. For modelling the HBV kinetics, we construct representative sinusoidal regions over the whole liver organ. Mathematical modelling techniques for computational tractability of HBV virus, to cell membrane receptors, and to cytokine signalling and cccDNA turnover are required to capture the complex infection process in single-cell models. The single-cell model and its distribution must then be incorporated into a representative sinusoidal system, where the spatial heterogeneity of receptor kick in, as well as Differing densities for immune cells (Kupffer, NK) at key spatial locations, thus affecting HBV infection distribution over a whole organ.

Fig. 3: A multiscale model scheme for HBV incorporating the spatial gradient of NTCP and gluconeogenesis. PP: Peri-portal; PC: Peri-central.

Modelling the rat liver

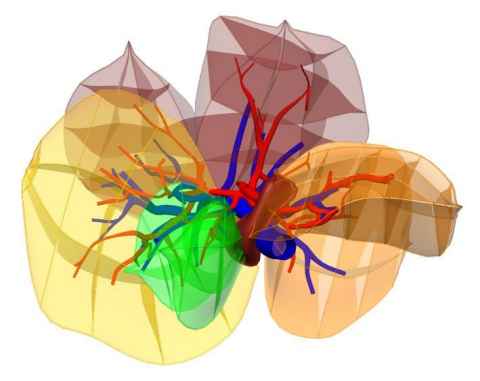
Rat livers are frequently used as the animal models for investigating liver functions, hepatobiliary surgical techniques, and drug efficacy. Many of these studies require an accurate understanding of the rat liver anatomy, including the lobular and vascular structures. In collaboration with Prof Dahmen of the Jene University, we have constructed an in silico rat liver atlas which is available to the modelling community (Fig. 4). Being consistent with the field modelling language FieldML, the geometric objects of the atlas can incorporate computational fields abstracted from numerical quantities such as blood flow, drug concentration, parenchymal elasticity properties etc for computations. For instance, the blood flow velocity and pressure pre- and post-lobectomy can be simulated by solving flow equations formulated on the portal and venous trees, and thus aid parenchyma regeneration analysis.